근본없는 코딩
[알고리즘] 정렬 알고리즘(버블/선택/삽입/합병/퀵) 본문
[ 정렬(Sort) 알고리즘 ]
버블정렬, 선택정렬, 삽입정렬, 합병정렬, 퀵정렬
00. Big O 표기법과 시간 복잡도
. 시간 복잡도: 알고리즘의 수행시간을 의미하는 지표
. 공간 복잡도: 알고리즘의 메모리 사용량
✔️ 빅오(Big O) 표기법
. O(n): 이 함수는 n만큼의 데이터가 주어졌을 때, '최악'의 경우 n만큼의 리소스를 소모한다.

✔️ 정렬 알고리즘
. 정렬 알고리즘: 어떤 데이터 셋이 주어졌을 때 이를 정해진 순서대로 나열하여 재배치하는 문제.

. 단순(구현 간단) 하지만 비효율적인 방법: 삽입정렬, 선택정렬, 버블정렬
. 복잡하지만 효율적인 방법: 퀵정렬, 힙정렬, 합병정렬, 기수정렬

01. 버블정렬(Bubble Sort)

✔️ 개념
. 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
. 첫번째와 두번째, 두번째와 세번째, 세번째와 네번째 ... 이런 식으로 마지막-1번째와 마지막 자료를 비교하고 교환하며 자료를 정리한다.
. 1회전이 끝나면 가장 큰 자료가 맨 뒤로 이동하므로, 2회전에서는 맨 끝의 자료는 제외하고 수행하게 된다.
. 정렬 1회전 수행 시마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.

✔️ 특징
. 장점: 구현이 간단하다.
. 단점: 시간복잡도가 최악이다.
. 시간 복잡도: O(n^2) 이며, Worst/Average/Best 모두 동일하다.
# include <stdio.h>
# define MAX_SIZE 5
// 버블 정렬
void bubble_sort(int list[], int n){
int i, j, temp;
for(i=n-1; i>0; i--){
// 0 ~ (i-1)까지 반복
for(j=0; j<i; j++){
// j번째와 j+1번째의 요소가 크기 순이 아니면 교환
if(list[j]<list[j+1]){
temp = list[j];
list[j] = list[j+1];
list[j+1] = temp;
}
}
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {7, 4, 5, 1, 3};
// 버블 정렬 수행
bubble_sort(list, n);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
02. 선택정렬 (Selection Sort)

✔️ 개념
. 데이터 중 가장 작은 값의 데이터를 선택하여 앞으로 보내는 정렬
. 입력배열(정렬되지 않은 값들) 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
. 주어진 배열 중 최솟값을 찾는다 → 그 값을 맨 앞에 위치한 값과 교체한다 → 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다 → 하나의 원소만 남을 때까지 앞의 과정을 반복한다.
✔️ 특징
. 장점: 자료 이동 횟수가 미리 결정된다.
. 단점: 값이 같은 레코드가 있는 경우에 상대적인 위치가 변경될 수 있다.
. 시간복잡도: O(n^2)이며, Worst/Average/Best 모두 동일하다.

03. 삽입정렬 (Insertion Sort)
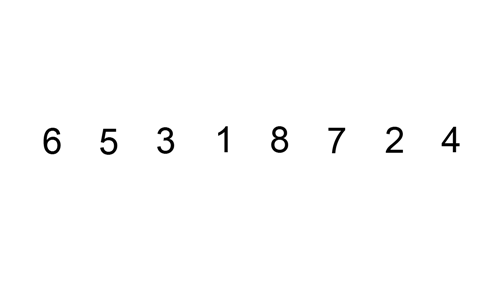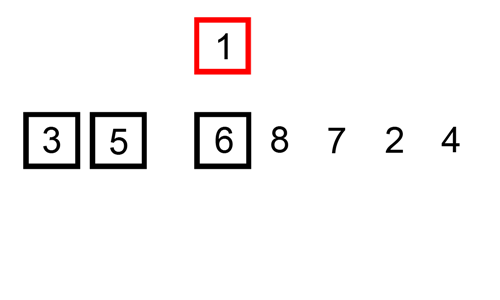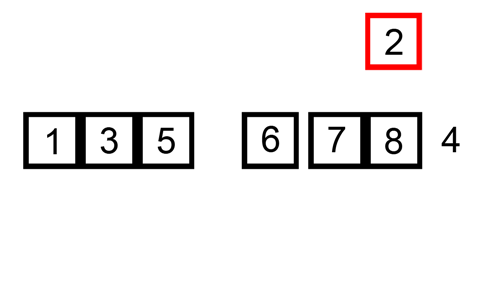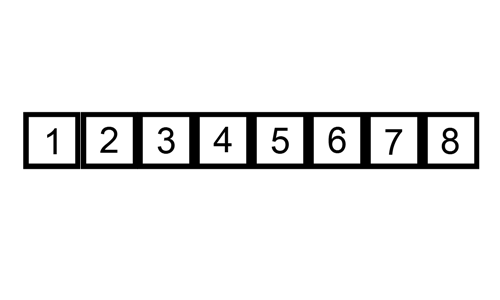
✔️ 개념
. 데이터를 순서대로 뽑아서 적절한 위치를 찾아 삽입함으로써 완성하는 정렬
. 손 안의 카드를 정렬하는 방법과 유사하다.
. 두 번째 자료부터 시작하여, 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고, 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘.
✔️ 특징
. 장점: 레코드가 이미 정렬되어 있는 경우 매우 효율적
. 단점: 레코드 수가 많고 크기가 클 경우 적합하지 않다.
. 시간복잡도: O(n^2)이며, Worst/Average는 동일하고, Best의 경우 O(n)이다. → 이미 정렬된 데이터가 많다면 빠른 알고리즘.

04. 합병정렬 (Merge Sort)

✔️ 개념
. '분할, 정렬, 결합' 순으로 진행되는데, 데이터 배열을 2개 이상의 부분 배열로 분할하고, 부분배열에서 정렬을 한 뒤 결합하여 다시 정렬을 진행한다.
. 데이터 배열 전체가 다시 결합되고 정렬되며 마친다.
. 분할 정복(divide and conquer) 알고리즘의 하나이다.
. 리스트의 길이가 0또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는 → 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다. → 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다. → 두 부분의 리스트를 다시 하나의 정렬된 리스트로 합병한다.
① 분할(입력 배열을 같은 크기의 2개의 부분 배열로 분할)
② 정복(부분 배열을 정렬, 크기가 충분히 작지 않으면 순환호출)
③ 결합(정렬된 부분 배열들을 합병)
✔️ 특징
. 장점: 데이터의 분포에 영향을 덜 받는다(입력데이터가 무엇이든 정렬 시간 동일), 만약 연결리스트로 구성하면, 데이터의 이동은 작아진다(=제자리 정렬로 구현). → 크기가 큰 레코드를 정렬할 경우 연결리스트를 사용하면 효율적인 방법.
. 단점: O(n) 수준의 메모리가 추가로 필요하다.
. 시간복잡도: O(n log n)이며, Worst/Average/Best 모두 동일하다.

05. 퀵정렬 (Quick Sort)

✔️ 개념
. 임의의 기준 값(피벗, pivot)을 정해서 두 부분집합으로 나눈다.
. 왼쪽은 피벗보다 작은 값, 오른쪽은 피벗보다 큰 값을 배치하고 더 이상 집합을 나눌 수 없을 때까지 재귀적으로 실행된다.
. 분할 정복 방법이며, 합병 정렬의 경우 분할 후 합병시에 정렬을 하지만, 퀵정렬은 분할 시에 정렬을 한다고 보면 된다.
. 리스트 안에 있는 한 요소(피벗, pivot)을 선택한다. → 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고, 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다 → 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 분할하여 다시 정렬한다(재귀) → 부분 리스트들이 더이상 분할이 불가능 할때까지 반복한다.
① 분할: 입력 배열을 피벗 기준으로 비균등하게 2개의 부분배열(왼쪽-피벗보다 작은 요소들, 오른쪽-피벗보다 큰 요소들)로 분할한다.
② 정복: 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환호출을 이용하여 다시 적용한다.
③ 결합: 정렬된 부분 배열들을 하나의 배열에 합병한다.
✔️ 특징
. 장점: 속도가 빠르며, 추가 메모리 공간을 필요로 하지 않는다.
. 단점: 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 오히려 수행 시간이 더 많이 걸린다.
. 시간복잡도: O(n log n)이며, Average/Best는 동일하고, Worst의 경우 O(n^2)이다. → 이미 정렬된 데이터라면 매우 비효율적으로 작용한다.

06. 힙정렬 (Heap Sort)

✔️ 개념
. 이진트리 기반의 트리형 자료구조로써, 최솟값이나 최댓값을 찾아내기 위해 사용한다.
. 내림차순 정렬 == 최대힙, 오름차순 정렬 == 최소힙
✔️ 특징
. 장점: 시간 복잡도가 좋은 편이며, 가장 큰 값 몇개만 필요할 때 유용하다.
. 시간복잡도: O(n log n)이며, Worst/Average/Best 모두 동일하다.
📌 참고자료/출처
. https://evan-moon.github.io/2018/10/13/sort-algorithm/
. https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
. https://aiday.tistory.com/53
. https://ko.wikipedia.org/wiki/%ED%95%A9%EB%B3%91_%EC%A0%95%EB%A0%AC
. https://hongjw1938.tistory.com/31
. https://ko.wikipedia.org/wiki/%ED%9E%99_%EC%A0%95%EB%A0%AC
'✔ Algorithm' 카테고리의 다른 글
| [자료구조] 배열, 스택, 큐, 연결 리스트, 트리, 해시 테이블, 그래프 (1) | 2023.12.18 |
|---|---|
| [알고리즘] Segment Tree (2) | 2023.06.09 |
| [알고리즘] Array - 완전 검색, 탐욕 알고리즘 (0) | 2023.05.29 |



