근본없는 코딩
[알고리즘] Segment Tree 본문
01. Segment Tree(세그먼트 트리, 구간 트리) 란?
. 결과적으로 보면, 배열과 연산이 주어졌을 때 Binary Tree(이진트리)의 구조를 이용해서, 연속적인 배열의 부분을 연산했을 때의 정보를 미리 저장해놓고 빠르게 구하는 방법이다.
예를 들면, 배열에 아래와 같이 arr = [0, 1, 2, 3, 4, 5, 6, 7] 이 들어있다고 가정해보자.
arr[3]~arr[5]의 합을 구하라 한다면, arr[3]+arr[4]+arr[5]를 구하게 될 것이다.
|
index
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
arr
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
합을 구한 뒤, arr[4]가 10으로 변경되어 arr=[0,1,2,3,10,5,6,7]이 된 경우, 다시 arr[3]+arr[4]+arr[5]를 구하라고 한다면, 다시 덧셈을 진행해야한다.
|
index
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
arr
|
0
|
1
|
2
|
3
|
10
|
5
|
6
|
7
|
|
이에 대한 시간복잡도를 계산하게 되면, 수를 바꾸는데 O(1), 수를 더할 때 O(N), M번 수행 → O(MN)이 된다.
하지만 세그먼트 트리를 활용한다면, 시간복잡도가 급격히 줄어들게 된다. → O(MlgN)
02. 세그먼트 트리의 전체 크기 구하기
. N은 입력된 수의 크기라고 하자. (= 가장 밑단의 길이)
. 세그먼트 트리는 이진트리기 때문에, 전체 크기(배열 사이즈)를 구하기 위해서는 2^k로 N보다 바로 큰 값을 만들 수 있는 k를 구해야 한다. 그 2^k 값에 *2를 하면 원하는 세그먼트 트리를 구할 수 있다.
. 다만 귀찮으니, N * 4 를 하면 메모리가 조금 더 크게 잡힐 수 있긴 하지만 편하게 이용할 수 있다.
03. 세그먼트 트리의 노드 의미 및 번호
. 세그먼트 트리의 리프노드와 리프노드가 아닌 노드는 다음과 같은 의미를 갖게 된다.
|
✔️ 리프노드: 배열의 그 수 자체
✔️ 리프노드가 아닌 노드: 왼쪽 자식과 오른쪽 자식의 합(혹은 다른 주어진 연산)
|
또한 이진 트리이기 때문에, 배열로 이 트리를 형성할 것이고,
선택한 노드의 번호가 x라면 왼쪽 자식의 번호는 2x, 오른쪽 자식의 번호는 2x+1 된다.

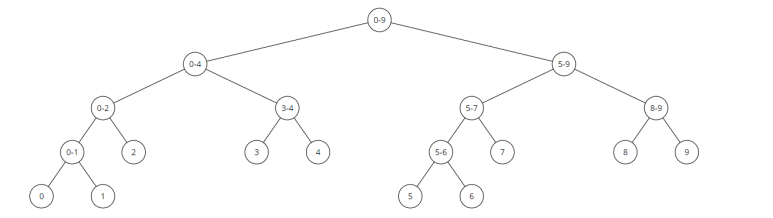
위 그림은 N=10일 경우의 세그먼트 트리다.
① [x-y]의 값이 들어있는 노드는, 리프노드가 아닌 노드로, 구간을 의미한다.
→ 만약 주어진 연산이 합이라면, 이 노드에 x~y의 합이 들어가있을 것이다.
② [x] 의 값이 들어있는 노드는, 리프노드로 주어진 배열의 값이 들어가 있다.

각 노드의 번호를 그림에 표기하면 위와 같다.
내가 선택한 노드가 4번 노드라면 그 왼쪽 자식의 노드 번호는 8(=2*4), 오른쪽 자식의 노드 번호는 9(=2*4+1)가 되는 것이다.

그 원리는 위 그림을 보며 설명할 수 있는데,
우리는 배열로 세그먼트 트리를 형성하기 때문에, 가장 루트 노드를 1번으로 생각할 것이다.
그 다음으로 루트노드(1)의 왼쪽 자식(2)과 오른쪽 자식(3)이 들어갈 것이다.
그럼 그 뒤로, 2의 왼쪽자식(4)과 오른쪽자식(4), 3의 왼쪽자식(5)과 오른쪽자식(6)이 들어갈 것이다.
세그먼트 트리는 full binary tree에 가깝기 때문에, 배열의 모든 값이 채워져 있을 가능성이 높고, 따라서 각 노드마다 왼쪽/오른쪽 자식 노드가 규칙적으로 위치하게 되는 것이다.
|
✔️ 노드의 왼쪽 자식 배열 번호: 2 * 현재노드번호
✔️ 노드의 오른쪽 자식 배열 번호: 2 * 현재노드번호 + 1
|
04. 구간 합을 구하는 방법
구간 left, right가 주어졌을 때, 합을 구하려면 트리를 루트부터 순회하며 각 노드에 저장된 구간의 정보와 left, right와의 관계를 살펴봐야 한다.
① node에 저장된 구간 = [start, end]
② 내가 합을 구하려는 구간 = [left, right]
✔️ Case 1. [start, end]가 [left, right]를 완전히 포함하는 경우
. 예를 들면, 현재 루트노드(start=0, end=9)에 위치하고 있는데 내가 2~7(left=2, right=7)의 합을 구하려고 하는 경우다.
→ 이 경우 왼쪽 자식과 오른쪽 자식을 루트로하는 트리에서 다시 탐색을 시작해야 한다.
✔️ Case 2. [start, end]가 [left, right] 안에 포함되는 경우
. if (left <= start && end <= right) 와 같은 경우다.
. 이 경우, 더 이상 탐색을 이어나갈 필요가 없다. 구해야 하는 합의 범위는 [left, right]인데, [start, end]는 그 범위에 모두 포함되고, 그 note의 자식도 모두 포함되기 때문에, 더 이상의 하위 호출은 비효율적이다. 따라서 tree[node]를 리턴해 탐색을 종료한다.
✔️ Case 3. [start, end]와 [left, right]가 겹치지 않는 경우
. if (left > end || right < start) 와 같은 경우다.
. left > end는 내가 찾고자 하는 범위의 가장 작은 값이 노드의 가장 큰 값보다 큰 경우이고, right < start는 내가 찾고자 하는 범위의 가장 큰 값이 노드의 가장 작은 값보다 작은 경우이다. 따라서 겹치지 않기 때문에, 이 아래의 노드들도 다 내가 찾고자 하는 범위에 해당되지 않으니 0을 리턴하며 탐색을 종료하면 된다.
✔️ Case 4. [start, end]와 [left, right]가 겹쳐져 있는 경우 (Case 1,2,3 제외한 나머지 경우)
. Case 1과 마찬가지로 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 시작해야 한다.
예를들어, N=10, left = 2, right = 4인 경우 합을 구하는 과정을 생각해보자.

1) 우선 1번 노드인 루트 노드[0, 9] 에 방문하게 된다.
. Case 1번으로, 왼쪽/오른쪽 자식 노드를 다시 탐색해야한다.
2) 그럼 우선 왼쪽 자식 노드로 가보자. 2번 노드[0, 4] 를 방문해본다.
. 동일하게 Case 1번으로, 왼쪽/오른쪽 자식 노드를 다시 탐색해야한다.
3) 그럼 다시 2번노드의 왼쪽 자식노드부터 방문해보자. 4번 노드[0, 2]를 방문해본다.
. Case 4번으로, 왼쪽/오른쪽 자식 노드를 다시 탐색해야한다.

4) 4번 노드의 왼쪽 자식 노드는 8번노드[0, 1]이다.
. Case 3번으로, 겹치지 않으니 0을 리턴한다.
5) 4번 노드의 왼쪽 자식 노드에서 리턴이 왔으니, 다음으로 오른쪽 자식 노드인 9번노드[2] 로 이동해보자.
. 리프노드로 [2,2]로 보면 되며, Case 2번으로 tree[node]를 리턴한다.
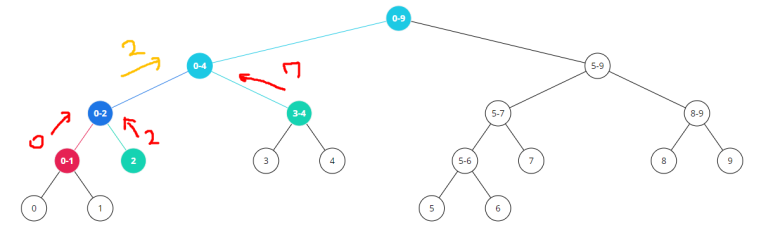
6) 4번노드의 왼/오른쪽 자식들 탐색이 끝났으니, 다시 2번 노드로 올라가본다.
7) 2번 노드의 오른쪽 자식의 노드인 5번 노드[3-4] 로 가보자
. 완전히 포함되는 범위이니 Case 2번으로, tree[node] = 7 을 리턴하며 이 아래 부분의 탐색은 종료한다.

8) 루트노드의 왼쪽 자식인 2번노드도 탐색이 끝났으니, 다시 루트노드로 올라간다.
9) 이번엔 루트노드의 오른쪽 자식인 3번노드[5, 9]의 탐색을 시작해본다.
. 3번 노드의 경우 Case 3번으로, 찾으려는 범위에 전혀 포함되지 않으니 0을 리턴하며 탐색을 종료한다.
그럼 최종적으로 9로 끝!
05. 원하는 위치의 값 변경하기
index번째 수를 val로 변경하는 경우에는, index 번째를 포함하는 노드에 들어있는 합만 변경해주면 됩니다. 원래 index 번째 수가 a[index] 였고, 바뀐 수가 val이라 하면, 노드에 들어있는 합은 diff(= val - a[index]) 만큼 변하게 됩니다.
✔️ Case 1. [start, end]에 index가 포함되는 경우
. 재귀 호출을 통해 index를 찾으러 들어간다.
✔️ Case 2. [start, end]에 index가 포함되지 않는 경우
. 재귀 호출을 중단한다.
① 리프 노드를 찾을 때 까지, 재귀호출을 이어간다.
② 리프 노드를 찾으면, 그 노드의 합을 변경하고 리턴한다.
③ 이후, 리턴될 때마다 각 노드의 합을 자식에 저장된 합을 이용해 다시 구해서 업데이트 한다.
'✔ Algorithm' 카테고리의 다른 글
| [자료구조] 배열, 스택, 큐, 연결 리스트, 트리, 해시 테이블, 그래프 (1) | 2023.12.18 |
|---|---|
| [알고리즘] 정렬 알고리즘(버블/선택/삽입/합병/퀵) (0) | 2023.06.25 |
| [알고리즘] Array - 완전 검색, 탐욕 알고리즘 (0) | 2023.05.29 |



