근본없는 코딩
나이브 베이즈 추천 알고리즘 본문
Contents-based Recommender System
나이브 베이즈 추천 알고리즘
📌 확률(Probability)
- 사건(Event) A가 발생할 가능성
- P(A) = 사건 A의 경우의 수 / 전체 경우의 수
📌 조건부 확률(Conditional Probability)

📌 베이즈 정리(Bayes' Theorem)



. Confusion Matrix
→ Training을 통한 Prediction 성능을 측정하기 위해 예측 value와 실제 value를 비교하기 위한 표
→ TP와 TN은 실제 값을 맞게 예측한 부분이며, FP와 FN은 실제 값과 다르게 예측한 부분을 의미
① TP (True Positive): 예측을 Positive로 했는데, 맞춘 경우
② TN (True Negative): 예측을 Negative로 했는데, 맞춘 경우
③ FP (False Positive): 예측을 Positive로 했는데, 틀린 경우
④ FN (False Negative): 예측을 Negative로 했는데, 틀린 경우


- Recall: 실제가 Positive인 경우(TP + FN)만 고려했을 때, 얼마나 정확한 예측을 했는지에 대한 지표
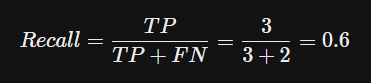

- Percision(정밀도): 모델이 Positive라고 예측한 경우(TP+FP)만 고려했을 때, 얼마나 정확한 예측을 했는지에 대한 지표


➕ 베이즈정리 이해하기
1) 배경 상황
. 수학자 W씨가 발렌타인데이에 호감이 있던 사람에게 초콜렛을 받았다.

. 하지만 W씨는 신중한 성격이라, 상대방이 호감이 있어서 초콜렛을 준건지 그냥 예의상 준건지 확신할 수가 없다.
→ 초콜렛을 받았기 때문에 상대방이 나를 좋아할 확률이 더 높아졌는지 계산해보자!

2) 사전확률
. 상대방에게 직접 물어보기 전에는 상대방이 W씨를 좋아하는지 안좋아하는지 알 수 없으므로, 좋아할 확률도 50%, 좋아하지 않을 확률도 50%로 가정하자.
→ 참고) 아무 정보가 없는 상황에서 확률을 동등하게 생각하는 것 = 이유 불충분의 원리 (by. 라플라스)

2-1) 추가 정보
. 계산을 하기 위해, 설문조사 등을 참고하여 정보 2개를 알아낸다.
① 좋아하는 사람일 때, 초콜릿을 줄 확률

② 호감이 없는 사람에게 예의상 초콜릿을 줄 확률

→ 설문조사를 통해 알아냈다고 가정해본다면,
CASE 1. 좋아하는사람에게 초콜렛을 줄 확률 40% → 자연스럽게 좋아하지만 초콜렛을 주지 않을 확률 60%
CASE 2. 예의상 초콜렛을 줄 확률 30% → 예의상으로라도 초콜렛을 주지 않을 확률 70%

(예시) 100명의 사람
STEP 1. 이유불충분의 원리에 따라 50명은 누군가에게 호감을 얻고있고, 50명은 인기가 없다.

STEP 2. 호감을 얻고 있는 50명 중 40%인 20명은 초콜렛을 받는다. (①)
→ 호감을 얻고있는 50명의 60%인 30명은 초콜렛을 못받는다. (②)
STEP 3. 인기가 없는 50명 중 30%인 15명은, 예의상 초콜렛을 받고 헛된 희망을 품는다. (③)
→ 나머지 70%인 35명은 초콜렛을 못받는다. (④)

3) 우리의 관심은?
. 우리가 알고자 하는것은 "초콜렛을 받았을 때, 초콜렛을 준 사람이 날 좋아할 확률"
== 우리가 알고 있는 정보인 "좋아하는 사람일 때, 초콜렛을 줄 확률"의 조건과 결과가 뒤바뀐 것

4) 불필요한 상황 제거
. 초콜렛을 못받은 상황은 우리의 관심사가 아니므로 제거한다.

5) 원하는 확률 구하기
. 초콜렛을 받은 사람은 총 35명
. 이 중 관심있어서 초콜렛을 받은 사람은 20명

→ 이 비율을 계산하면? 20/35*100 = 57%

6) 결론
. W씨는 상대방이 나에게 관심을 갖고 있을 확률을 50%에서 57%로 업데이트 할 수 있다.
. 아무런 정보 없이 50%라고 생각했던 값은 "사전확률"
. 초콜렛을 주었다는 새로운 정보 덕분에 얻은 57%값은 "사후확률"

. 베이즈 정리 == 사전 확률을 바탕으로 사후 확률을 얻는 것


. 출처: https://www.youtube.com/watch?v=Y4ecU7NkiEI
📌 나이브베이즈 분류기(Naïve Bayes Classifier)
. Naïve의 사전적 의미 = '(모자랄 정도로) 순진한'
. 사전적 의미를 덧붙여 해석하면 그냥 단순하고 순수하게 Bayes분석을 한다로 볼 수 있습니다.
→ 분류를 쉽고 빠르게 하기 위해 분류기에 사용하는 특징(feature)들이 서로 확률적으로 독립이라는 순수함이 가정으로 들어갔기 때문이라 생각
1) 나이브 베이즈 작동 방식

① 베이즈 정리 (Bayes' Theorem)
. 나이브 베이즈(Naive Bayes) 분류기는 베이즈 정리를 사용하여 클래스의 확률을 계산합니다.
② 나이브 가정 (Naive Assumption)
. Naive Bayes 분류기의 "나이브" 부분은 입력 변수들이 서로 독립적이라는 가정에 기반합니다.
. 이것은 현실에서는 거의 충족되지 않는 경우가 많지만, 모든 변수 간의 조건부 독립성 가정을 하면 계산이 간단해집니다.
③ 학습 (Training)
. Naive Bayes 분류기는 훈련 데이터를 사용하여 클래스별 사전 확률 (P(C))과 각 클래스에 대한 변수들의 조건부 확률 (P(X∣C))을 추정합니다. 이때, 변수들은 입력 데이터의 특징을 나타냅니다.
④ 분류 (Classification)
. 새로운 입력 데이터가 주어지면, 각 클래스에 대한 사후 확률 (P(C∣X))을 계산하고, 가장 높은 사후 확률을 가지는 클래스를 선택하여 분류합니다. 즉, 다음과 같이 계산합니다.
C 결정 = argmaxC P(C∣X) = argmaxC P(X∣C)⋅P(C) / P(X)
2) 영화 추천 시스템으로 보는 특징

. 아이템 특징(feature, attribute 등)끼리 서로 독립
→ 나이브베이즈의 가정.
. 영화 장르와 영화 감독이 서로 연관이 없는 특징이어야 한다.
→ 나이브베이즈의 가정.
. 데이터 셋이 커도 모델 예측에 관계 없다
→ 아이템의 특징을 가지고 데이터 셋의 조건부 확률을 구하는 것일 뿐이므로 모델이 크더라도 상관은 없다.
. Continuous Variable보다 Discrete Variable에 더 잘 맞는다.
→ Continuous로 0과 1사이에 0.7, 0.5 이런식으로 데이터가 있다보면 그 feature가 독립이라는 가정을 세우기 어렵다.
→ Discrete로 0과 1로 구분한다면 독립으로 볼 수 있다.
. 간단하고, 계산량이 많지 않은 모델
. 데이터의 차원이 높아질수록 모든 class에 대해 확률이 0으로 수렴 가능(Laplace Smoothing 활용)
→ 숫자를 더해서 확률이 0으로 가는것을 방지하는 기법

Class j: 영화가 좋다 → 이에 따른 x라는 feature, x`은 새로운 feature
. 위 수식은 베이즈정리의 수식과 동일함을 알 수 있다.
. 이 수식을 바탕으로 '모든 feature는 독립이다'라는 가정을 바탕으로 P(x|Class j)의 확률을 나머지들의 곱으로 알 수 있다.
→ 독립일 경우 각 확률을 곱할 수 있기 때문
. 윗 부분은 모델을 확습시키는 과정, 아래 부분은 학습된 상태를 바탕으로 어느 Class에 속할지 예측하는 과정
(예제) 밖에서 나가 놀지 말지 예측 (날씨, 온도, 습도, 바람)


➕ 나이브 베이즈 분류기 이해하기 - 넷플릭스 추천 알고리즘
1) Cold Start

. Cold Start: 아무 정보도 없는 상태
. 처음 가입한 시청자에 대해서는 아무런 정보가 없는 상태이므로, 영화를 좋아할 확률을 50%로 가정(사전확률)



2) 1차 진행 (10편의 영화)
. 시청자는 총 10편의 영화를 보았다고 한다.

. 5개의 좋아요를 눌렀는데, 이 중 3개가 Action 영화였다. == 좋아하는 영화 중 60%가 액션 장르
. 5개의 싫어요를 눌렀는데, 이 중 1개가 Action 영화였다. == 싫어하는 영화 중 20%가 액션 장르

. 베이즈 정리의 사각형으로 표현해본다면?
① 가로 세로 1인 사각형을 그리고, 가로 길이에 영화를 좋아할 확률(50%)/싫어할 확률(50%)로 가정했던 사전확률을 놓는다.

② 왼쪽 세로는 좋아하는 영화일 때 그 영화가 액션 장르일지 아닌지로 구분
③ 오른쪽 세로는 싫어하는 영화일 때 그 영화가 액션 장르일지 아닌지로 구분

④ 사각형의 넓이를 구하면 각 경우의 확률

⑤ 이를 기반으로 시청자가 액션영화를 봤을 때 좋아요를 누를 확률 = 75% 를 구할 수 있다.

2-1) 1차 진행의 업데이트 결과
. 시청자가 액션영화를 봤을 때 좋아할 확률은 75%로 업데이트 되었다.
→ 넷플릭스는 시청자에게 액션영화를 많이 추천할 것이다.


3) 2차 진행
. 이번에는 넷플릭스 인공지는이 장르가 아닌 출연배우에만 주목했다고 가정
. 마찬가지로 시청자는 10편의 영화를 추가로 보았고, 좋아요 5개와 싫어요 5개를 눌렀다.

. 좋아요를 누른 영화 5편 중 4편이 라이언 레이놀즈가 나온 영화였다.
→ 이 시기에 좋아한 영화의 80%에는 라이언 레이놀즈가 나왔다.
. 싫어요를 누른 영화 5편 중 1편이 라이언 레이놀즈가 나온 영화였다.
→ 이 시기에 싫어한 영화의 20%에는 라이언 레이놀즈가 나왔다.

4) 학습 내용을 바탕으로 좋아할 확률 구하기
. 만약 어떤 액션영화에 라이언 레이놀즈가 출연한다면 시청자는 이 영화를 얼마나 좋아할까?
① 1차 진행을 통해 액션영화일 때, 이 영화를 좋아할 확률은 75%라는 것을 알고있다.

② 2차 진행을 통해 좋아한 영화의 80%는 라이언 레이놀즈가 나왔고, 싫어한 영화의 20%는 라이언 레이놀즈가 나왔다는 사실을 알고 있다.

③ 위 사각형을 기반으로 액션 장르이고 라이언 레이놀즈가 출연한 영화를 시청자가 얼마나 좋아할 지 계산할 수 있다.
→ 92.3%


5) 넷플릭스 학습



. 출처: https://www.youtube.com/watch?v=me--WQKQQAo
'✔ etc.' 카테고리의 다른 글
| TF-IDF로 장르, 영화 tag이용한 추천 알고리즘 실습 (1) | 2024.05.01 |
|---|---|
| TF-IDF란? (0) | 2024.05.01 |
| [System] DR(Disaster Recovery, 재해복구시스템) (0) | 2023.06.25 |
| HTTP1.1, HTTP2 그리고 QUIC (0) | 2023.06.20 |




